Question

Farmer Ed has 650 meters of fencing, and wants to enclose a rectangular plot that borders on a river.maximize the area. What is the largest area that can be enclosed?Farmer Ed does not fence the side along the river, find the length and width of the plot that will maximize the area.What is the largest area that can be enclosed?

Answer 1

We have the next equation for the Area

the formula for the area is

`A=l* w`

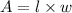
l=650-2x

w=x

then we substitute the values

`A=(650-2x)(x)`
`A=650x-2x^2`

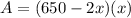
the maximum value of x is the vertex of the quadratic equation

where

a=-2

b=650

`x=(-b)/(2a)=(-650)/(2(-2))=(-650)/(-4)=162.5`

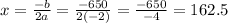
the largest area that can be enclosed is

`\begin{gathered} A=650(162.5)-2(162.5)^2 \\ A=105625-52812.5 \\ A=52812.5m^2 \end{gathered}`

l=650-2(162.5)=325m

w=162.5m