Answer
y - 4 = (-4/5) (x + 6)
We can then simplify further by multiplying through by 5
5y - 20 = -4 (x + 6)
5y - 20 + 20 = -4x - 24 + 20
5y = -4x - 4
Step-by-step explanation
The general form of the equation in point-slope form is
y - y₁ = m (x - x₁)
where
y = y-coordinate of a point on the line.
y₁ = This refers to the y-coordinate of a given point on the line
m = slope of the line.
x = x-coordinate of the point on the line whose y-coordinate is y.
x₁ = x-coordinate of the given point on the line
Now, we need to calculate the slope
For a straight line, the slope of the line can be obtained when the coordinates of two points on the line are known. If the coordinates are (x₁, y₁) and (x₂, y₂), the slope is given as
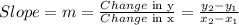
For this question,
(x₁, y₁) and (x₂, y₂) are (-6, 4) and (-1, 0)
x₁ = -6
y₁ = 4
x₂ = -1
y₂ = 0
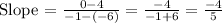
Slope = m = (-4/5)
We can then use any of the points given as the point in the equation
(x₁, y₁) = (-6, 4)
x₁ = -6, y₁ = 4
y - y₁ = m (x - x₁)
y - 4 = (-4/5) (x - (-6))
y - 4 = (-4/5) (x + 6)
We can then simplify further by multiplying through by 5
5y - 20 = -4 (x + 6)
5y - 20 + 20 = -4x - 24 + 20
5y = -4x - 4
Hope this Helps!!!