Question

Ben and Diane meet up to fly a model airplane they have built together. At full power, the airplanecan fly 160 kilometers per hour in calm air. Ben has the controls, and he makes the plane take offheading 25° North of East. After he feels comfortable with the controls, he turns on full power.9.A steady wind begins to blow from North to South at a speed of 32 kilometers per hour.In what direction and at what speed is the plane traveling now?

Answer 1

We have two opposing vectors, 160kph N of E and 32 kph S. In order to get the speed and direction of the plane, we have to add the vectors and solve for it's direction. In vector addition, we have to take the component in the x and in the y axis of each vectors and add all the x-components and all the y components.

To get the x component we have to multiply the magnitude of the vector with the cos of its angle with respect to the positive x axis.

X-component

X1 = 160 cos (25) = 145 kph

X2 = 32 cos (270)= 0 (you may also use -90 , moving clockwise from the positive x axis and you will get the same result)

Xtotal = 145 + 0 = 145 kph

To get the y component we have to multiply the magnitude of the vector with the sin of its angle with respect to the positive x axis.

Y1 = 160 sin (25) = 67.62 kph

Y2= 32 sin (270) = - 32 kph (you may also use -90 , moving clockwise from the positive x axis and you will get the same result)

Ytotal = 67.62 + (-32) = 35.62 kph

Now, for us to get the speed of the plane , we need to get the resultant of the vectors.

The resultant of the vectors i given by the formula:

`R=\sqrt[]{X^2_(total)+Y^2_(total)}_{}`
`R=\sqrt[]{145^2+35.62^2}=149.31`

In solving for the direction of the plane we have to use the formula:

`\tan \varnothing\text{ = }(Y_(total))/(X_(total))\text{ }\Rightarrow\text{ }\varnothing=\tan ^(-1)((Y_(total))/(X_(total)))`
`\varnothing=\tan ^(-1)((35.62)/(145))=13.80^(\circ)`

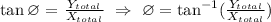
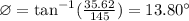
Answer:

The plane will be travelling at a speed of 149.31 kph heading 13.8 degrees North of East.