Question

In order for the parallelogram tobe a square, x = [? ].4x+17 126-23

Answer 1

For the given parallelogram to be a square, its diagonals should be equal. Let's put more details in the given figure to better understand:

Naming the two diagonals to be AC and BD, for it to be a square,

`\text{ AC = BD}`

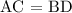
AC = 12x - 23

BD = 4x + 17

We get,

`\text{ AC = BD}`
`\text{ 12x - 23 = 4x }+\text{ 17}`
`\text{ 12x - 4x = 17 + 23}`
`\text{ 8x = 40}`
`\text{ }\frac{\text{8x}}{8}\text{ = }\frac{\text{40}}{8}`
`\text{ x = 5}`

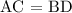
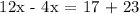
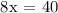
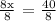
For the diagonals to be equal, x = 5.

Therefore, for it (parallelogram) to be a square, x should be equals to 5.

Let's check,

AC = 12x - 23 = 12(5) - 23 = 60 - 23 = 37

BD = 4x + 17 = 4(5) + 17 = 20 + 17 = 37