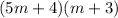Answer:
(5m+4)(m+3)
Explanation:
Given the quadratic expression:
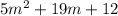
To factor the quadratic expression, follow the steps below:
Step 1: Multiply the coefficient of m² and the constant.

Step 2: Find two numbers that multiply to give 60, and add to give the coefficient of m, 19 To do this, list the factors of 60: 1,2,3,4,6,10,15,20,30, and 60.
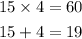
Step 3: Rewrite the middle term with those numbers.
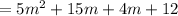
Step 4: Factor the first two and last two terms separately. Ensure that the expression in the brackets is the same.
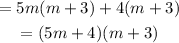
The factored form of the expression is: