To find angle between two lines, we use the formula,
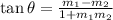
Where
θ is the angle between two lines
m1 is the slope of the first line
m2 is the slope of the second line
First Line Equation:
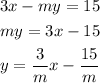
The slope is 3/m
Second Line Equation:
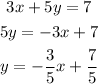
The slope is -3/5
The angle between the two lines is 45°.
Let's substitute the known information into the formula and figure out the value of 'm':
![undefined]()