The given function is:
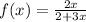
Graph the function as shown below:
As seen from the horizontal line test, the lines cut the function at only 1 point.
Hence the function is 1-1 and therefore invertible.
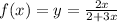
Solve for x to get:


Therefore replace y by x to get the required inverse function shown below:
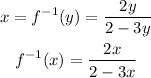
The inverse function is shown above.