We say that a set A is closed under a certain operation if
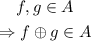
In our case,
a) It is evident that the polynomials are closed under addition and subtraction
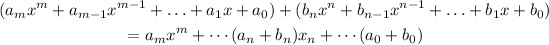
Which is a polynomial. Similarly, in the case of the multiplication of polynomials.
However, in the case of the division of polynomials, the result is not always a polynomial.
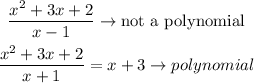
Thus, the set of polynomials is not closed under division.
b) Notice that the integers are closed under addition and subtraction (the integers are ...-2,-1,0,1,2,...).
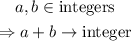
Similarly, in the case of the multiplication of integers.
Nevertheless, in the case of the division of integers,
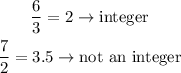
Therefore, the set of integers is not closed under division.
c) Rational numbers are numbers of the form a/b, where a and b are integers.

Once again, the set of rational numbers is closed under addition, subtraction and multiplication. As for the division of rational numbers,
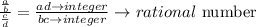
The rational numbers are also closed under division.
There are no restrictions for the set of rational numbers regarding operations.