Question

A company is designing a label for a new cylindrical container. The container and some of its dimensions are shown. The label will be the same height as the container and will not overlap itself and will cover the entire side of the cylinder. What will be the area of the label 2 A) 31(8.75) cm? B) 61(875) cm? 91(8.75) cm D) 127(8.75) cm2 E) 157t(8.75) cm?

Answer 1

The base area, B, of a cylinder with radius, r, is as given below

`B=\pi r^2`
`\begin{gathered} \text{ Since B = 9}\pi cm^2 \\ \text{then we must have that} \\ \pi r^2=9\pi \end{gathered}`

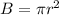
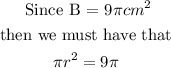
Hence,

Since the label will only cover the entire side of the cylinder without overlapping, then the area of the label is the curved surface area of the cylinder.

Given a cylinder with radius,r, and height, we must have that

`\text{the curved surface area = 2}\pi rh`

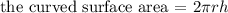
In this case, h = 8.75cm,

Therefore,

`\text{area of the label = 2}\pi*3*8.75=6\pi(8.75)cm^2`

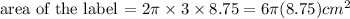
Hence the right choice is B