hello
to solve this question, let's write the standard equation of a straight line
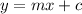
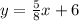
since, this equation passes the given gpoint and it's parallel to it, we will have to modify our equation
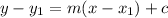
the given points are (0, 0)
let's insert it and solve
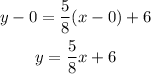
from the calculation above, the equation of the line is y = 5/8x + 6