Answer:
506.42 square yards.
Explanation:
In the diagram, all the shapes are regular polygons.
Area of Patio A
Patio A is a square with side length, s = 12 yards.
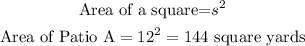
The area of Patio A is 144 square yards.
Area of Patio B
Patio B is a square with side length, s = 6.1 yards.
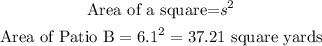
The area of Patio B is 37.21 square yards.
Area of the Hexagon
A regular hexagon can be divided into 6 equilateral triangles.
In the diagram:
• The base of one equilateral triangle = 12 yards
,
• The height of one equilateral triangle = 8 yards
The area of the hexagon therefore is:
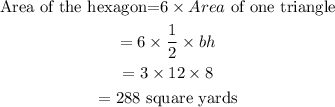
The area of the hexagon is 288 square yards.
Area of the Composite Figure:

The area of the composite figure is 506.42 square yards.