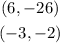Question

For each ordered pair (x,y) determine whether it is a solution to the inequality y<-3x-6

Answer 1

We have 4 ordered pairs (x,y), for which we must satisfy that the following inequality is satisfied:

`y<-3x-6`

What we must do to solve this is to replace the variables "x" and "y" in the inequality and verify that it is fulfilled.

First-order pair

`\begin{gathered} (7,-27) \\ -27<-3\cdot(7)-6 \\ -27<-21-6 \\ -27=-27 \end{gathered}`

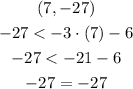
This order pair is not a solution to the inequality

Second-order pair

`\begin{gathered} (-9,25) \\ 25<-3\cdot(-9)-6 \\ 25<27-6 \\ 25>21 \end{gathered}`

This order pair is not a solution to the inequality

Third-order pair

`\begin{gathered} (6,-26) \\ -26<-3\cdot(6)-6 \\ -26<-18-6 \\ -26<-24 \end{gathered}`

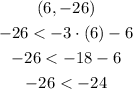
This order pair is a solution to the inequality

Fourth-order pair

`\begin{gathered} (-3,-2) \\ -2<-3\cdot(-3)-6 \\ -2<9-6 \\ -2<3 \end{gathered}`

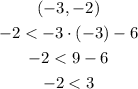
This order pair is a solution to the inequality

Finally, we have that only the following ordered pair are a solution for the inequality:

`\begin{gathered} (6,-26) \\ (-3,-2) \end{gathered}`