Question

A certain substance has a half-life of 2 minutes. A fresh sample of the substance weighing 60 mg was obtainedAfter how many minutes will there be 14 mg of the substance remaining?

Answer 1

`4.2\text{ minutes}`

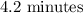
Step-by-step explanation:

Here, we want to get the number of minutes it will take for 14 mg of the substance to remain

We can have an exponential equation that describes the scenario as follows:

where A(t) is the amount remaining after t minutes

and t is the number of minutes

`\begin{gathered} A(t)=60(0.5)^{(t)/(2)} \\ ((14)/(60))^2=0.5^t \\ 0.054=0.5^t \\ \ln \text{ 0.054 = tln0.5} \\ t\text{ = }\frac{\ln \text{ 0.054}}{\ln \text{ 0.5}} \\ t\text{ = }4.2\text{ minutes} \end{gathered}`