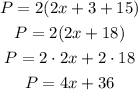Question

4. The figure below represents a section of a school. 15 gym cafelera a. Write an expression for the area of the gym. b. Write an expression for the area of the cafeteria. c. Write an expression for the total area of the gym and cafeteria. d. write an expression for the total perimeter of the gym and cafeteria.

Answer 1

a. The gym has the shape of a rectangle.

The area of a rectangle is calculated as follows:

`A=\text{base}\cdot\text{height}`

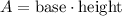
The base of the gym is x and its height is 15, then its area is:

`\begin{gathered} A=x\cdot15 \\ A=15x \end{gathered}`

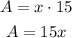
b. The cafeteria is a rectangle with a height of 15 and a base of (x+3), then its area is:

`\begin{gathered} A=(x+3)\cdot15 \\ \text{Distributing:} \\ A=x\cdot15+3\cdot15 \\ A=15x+45 \end{gathered}`

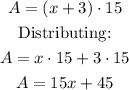
c. The total area is the addition of the gym area and the cafeteria area.

`\begin{gathered} A=15x+15x+45 \\ \text{Combining similar terms} \\ A=30x+45 \end{gathered}`

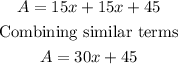
d. The perimeter of a rectangle is calculated as follows:

`P=2(base+height)`

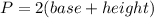
Considering both the gym and the cafeteria, the base is x + x + 3 = 2x + 3 units long. The height is 15, then:

`\begin{gathered} P=2(2x+3+15) \\ P=2(2x+18) \\ P=2\cdot2x+2\cdot18 \\ P=4x+36 \end{gathered}`