Question

A hickory nut is thrown straight down from a 10.m high window and lands on the ground with a velocity of 25.0m/s What was the initial velocity of the nut? How long was it in free fall?

Answer 1

Given data

*The given height is h = 10.0 m

*The given final velocity of the hickory nut is v = 25 m/s

*The value of the acceleration due to gravity is g = 9.8 m/s^2

The formula for the initial velocity of the nut is given by the equation of motion as

`v^2=u^2+2gh`

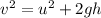
Substitute the known values in the above expression as

`\begin{gathered} (25)^2=u^2+2*9.8*10.0 \\ 625=u^2+196 \\ u^2=625-196 \\ u=20.71\text{ m/s} \end{gathered}`

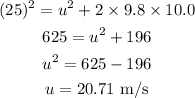
Hence, the initial velocity of the nut is u = 20.71 m/s

The formula for the time taken by the nut in free fall is given by the equation of motion as

`v=u+gt`

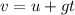
Substitute the known values in the above expression as

`\begin{gathered} 25.0=20.71+(9.8)t \\ t=0.43\text{ s} \end{gathered}`

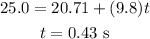
Hence, the time taken by the free fall is t = 0.43 s