Question

Quadrilateral ABCD will be translated 1 unit to the left and 4 units down. Then it will be dilated by ascale factor of 2 about the origin.1211109876BА643D7.891012511Z-8-53-8-4- 12 - 11 - 104-3-212-1 0- 1-2-3-4-5-6-7-8-9-10-11-12What is the location of point D after these transformations?O (-8, 12)(-8,-4)O (-2,-1)O (-2,3)

Answer 1

We have a figure to which we apply two transformations: a translation, 1 unit to the left and 4 units down, and a dilation by a factor of 2 about the origin.

We then can write the rules for a generic point (x,y) when this transformations are applied.

For a translation 1 unit to the left and 4 units down, it means that the x-coordinate is 1 unit less, as the left indicates smaller values, and the y-coordinate is 4 units less, as down indicates smaller values too. Then, the rule is:

`(x,y)\longrightarrow(x-1,y-4)`

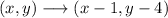
Now, a dilation of factor k around the origin can be written for a generic point (x,y) as:

`(x,y)\longrightarrow(kx,ky)`

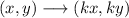
Then, if k=2 and we apply it to our transformed point we get:

`(x,y)\longrightarrow(x-1,y-4)\longrightarrow(2(x-1),2(y-4))=(2x-2,2y-8)`

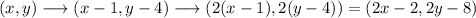
Then, the effect of the two transformations is:

`(x,y)\longrightarrow(2x-2,2y-8)`

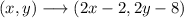
Applying this to the point D(-3,2) we get:

`D=(-3,2)\longrightarrow D^(\prime)^(\prime)=(2(-3)-2,2(2)-8)=(-6-2,4-8)=(-8,-4)`

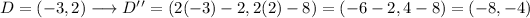
Answer: the transformed point D'' is (-8,-4) [Second option]