Question

The graph of h(x) is a translation of f(x)=√x.6h()(-1,1)7-6-5-4-2-1₁(-3,-1)2I b & I w to5 6 7 XWhich equation represents h(x)?Oh(x)=√√√x-2Oh(x) = √√√x + 2h(x) = 3√√x-2Oh(x) = √√x + 2

Answer 1

Given a function g(x), we can translate the graph by:

· A vertical shift. If we want to shift the function k units vertically:

`Vertical\text{ }shift:g(x)+k`

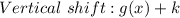
If k is negative, the shift is downwards. If k is positive, the shift is upwards.

·A horizontal shift. If we want to shift the function h units horizontally:

`Horizontal\text{ }shift:g(x+h)`

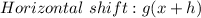
If h is positive, the graph shifts to the left. If h is negative, the graph shift to the right.

In the graph given, we know that:

`f(0)=\sqrt[3]{0}=0`

But g(-2) = 0. This means that the graph has a horizontal shift 2 units to the left.

As we have seen before, to shift two units to the left:

`\sqrt[3]{x}\text{ }shifted\text{ }2\text{ }units\text{ }left\Rightarrow\sqrt[3]{x+2}`

thus, the correct answer is the second optiion:

`h(x)=\sqrt[3]{x+2}`