Question

What is the graph of the solution to the following compound inequality?3-X22 or4x+2 2 10O A.-10 -9 -8 -7 -6 -5 4 -3 -2 -1 01 23456789 10O B.-10 -9 -8 -7-6 -5 -4 -3 -2 -101 2 3456789 10C.+-10 -9 -8 -7 -6 -5 -4 -3 -2 -10123+ 18 9 1045 67O D.-10 -9 -8 -7 -6 -5 -4 -3 -2 -10 1 2+8 9 10345 67

Answer 1

We have a compound inequality

`3-x\ge2\text{ or }4x+2\ge10`

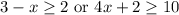
And we must graph its solution.

To graph the solution we need to solve the two inequalities of the compound inequality

1. 3 - x >= 2

To solve it we must:

- Subtract 3 from both sides

`\begin{gathered} 3-x-3\ge2-3 \\ \text{ Simplifying,} \\ -x\ge-1 \end{gathered}`

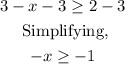
- Multiply both sides by -1.

We must bear in mind that when we have an inequality and we multiply or divide it by a negative number, the symbols change their meaning.

`\begin{gathered} -x\cdot-1\le-1\cdot-1 \\ \text{ Simplifying, } \\ x\le1 \end{gathered}`

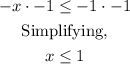
2. 4x + 2 >= 10

To solve it we must:

- Subtract 2 from both sides

`\begin{gathered} 4x+2-2\ge10-2 \\ \text{ Simplifying,} \\ 4x\ge8 \end{gathered}`

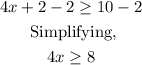
- Divide both sides by 4

`\begin{gathered} (4x)/(4)\ge(8)/(4) \\ \text{ Simplifying, } \\ x\ge2 \end{gathered}`

Finally, since the two inequalities has an 'or' means that the graph will be the graph will be the union of the solutions of each inequality

So, the correct answer is