Solve for the area of each faces, there are 6 faces, 2 of which are congruent.
Solving for area of surface 1
The first surface has a dimension of 9 ft by 6 ft, and is a rectangle. The volume is therefore is
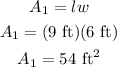
Solving for area of surface 2
The second surface has a dimension of 4 ft by 9 ft, and is also a rectangle. The volume is
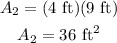
Solving for area of surface 3
The third surface has a dimension of the following
first base = 3 ft
second base = 6 ft
height = 3.7 ft
and is in the shape of trapezoid
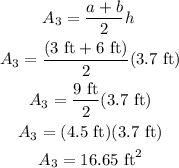
Solving for area of surface 4
The fourth surface has a dimension of 3 ft by 9 ft, and is in the shape of a rectangle
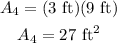
Solving for the surface area
To solve for the surface area, get the sum of the area of all the surfaces that is
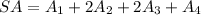
Note that surface 2 and surface 3 are multiplied by 2 since they have other faces that are congruent
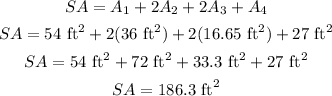
Therefore, the surface area of the figure is 186.3 square feet.