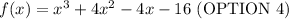Question

Find a polynomial with rational coefficients that has the given numbers as roots -4,-2, 2

Answer 1

We are told to find the polynomial that has the following roots -4, -2, 2.

Step-by-step explanation

- In order to solve this question in the easiest manner, we will make use of the following rules:

1. Sum of roots

2. Product of roots

3. Sum of Product of roots.

1. Sum of roots:

The sum of roots of a cubic equation is defined as follows:

`\begin{gathered} \text{Given the cubic equation:} \\ y=ax^3+bx^2+cx+d \\ \text{If the roots of the equation are: }\alpha,\beta,\gamma \\ \text{then,} \\ \\ \alpha+\beta+\gamma=-(b)/(a) \end{gathered}`

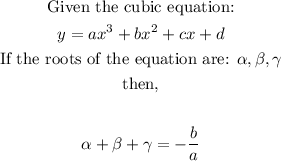
2. Product of roots:

The product of roots of a cubic equation is defined as follows:

`\alpha*\beta*\gamma=-(d)/(a)`

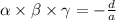
3. Sum of Product of roots:

`\alpha\beta+\alpha\gamma+\beta\gamma=(c)/(a)`

- We have been given these roots to be -4, -2, and 2. Thus, we can apply the 3 formulas defined above to find the correct equation.

- This is done below:

`\begin{gathered} Let\alpha=-4,\beta=-2,\text{ and }\gamma=2 \\ Also,\text{ let }a=1 \\ \\ -4+(-2)+2=-(b)/(a)=-(b)/(1) \\ -6+2=-b \\ \\ \therefore b=4 \\ \\ -4(-2)(2)=-(d)/(a)=-(d)/(1) \\ \therefore d=-16 \\ \\ -4(-2)+(-4)(2)+(-2)(2)=(c)/(a)=(c)/(1) \\ 8-8-4=c \\ \\ \therefore c=-4 \end{gathered}`

Now that we have all the coefficients, we can write out the equation as follows:

`f(x)=x^3+4x^2-4x-16`

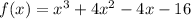
Final Answer

The answer is

`f(x)=x^3+4x^2-4x-16\text{ (OPTION 4)}`