Question

1. Use a calculator to find each angle measure to the nearest degree.a) sin A = 0.4848b) cos Y = 0.7431c) cos X = 0.4226d) tan B = 19.0811

Answer 1

Given

a) sin A = 0.4848

b) cos Y = 0.7431

c) cos X = 0.4226

d) tan B = 19.0811

To find:

Each angle measure to the nearest degree.

Step-by-step explanation:

It is given that,

a) sin A = 0.4848

b) cos Y = 0.7431

c) cos X = 0.4226

d) tan B = 19.0811

That implies,

a) sin A = 0.4848.

Then,

`\begin{gathered} A=\sin^(-1)(0.4848) \\ =28.99\degree \\ =30\degree \end{gathered}`

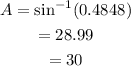
b) cos Y = 0.7431.

Then,

`\begin{gathered} Y=\cos^(-1)(0.7431) \\ =42.0038\degree \\ =42\degree \end{gathered}`

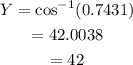
c) cos X = 0.4226.

Then,

`\begin{gathered} X=\cos^(-1)(0.4226) \\ =65.001\degree \\ =65\degree \end{gathered}`

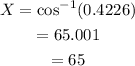
d) tan B = 19.0811.

Then,

`\begin{gathered} B=\tan^(-1)(19.0811) \\ =86.99\degree \\ =87\degree \end{gathered}`

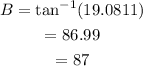
Hence, the measure of each angle is,

a) A = 30°.

b) Y = 42°.

c) X = 65°.

d) B=87°.