Question

Choose which of the following demonstrate a dilation centered at the origin: (x,y)→(1.5x,1.5y)

Answer 1

To answer this question, we need to remember that for a dilation centered a the origin, we need to multiply each of the given coordinates by the factor of dilation. In this case, we have that this factor is k = 1.5. This implies that the image is 1.5 greater than the original figure.

We have four graphs, in which:

1. Graph A implies that image A'B'C' is smaller than the original figure. Then, this is not the graph.

2. Graph B implies another kind of transformation. It is not a dilation.

3. We have that graphs C and D are the potential graphs to solve the question.

We need to identify the coordinates of the original figure:

`A(4,5),B(0,2),C(1,-1)`

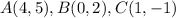
These are the coordinates for the original figure in both graphs.

Now, to have the corresponding dilation centered at the origin, we need to multiply each of the coordinates by the factor of dilation, k = 1.5. Then, we have:

`A(4,5)\rightarrow A^(\prime)(4\cdot1.5,5\cdot1.5)=A^(\prime)(6,7.5)`
`B(0,2)\rightarrow B^(\prime)(0\cdot1.5,2\cdot1.5)=B^(\prime)(0,3)`
`C(1,-1)\rightarrow C^(\prime)(1\cdot1.5,-1\cdot1.5)=C^(\prime)(1.5,-1.5)`

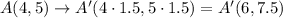
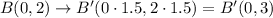
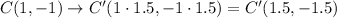
Now, we need to check these results for each graph.

We can see that:

Graph C fits the dilation centered at the origin indicated above.

Therefore, the answer to this question is C (graph represented by letter C).