Answer
Normal distribution, also called Gaussian distribution, the most common distribution function for independent, randomly generated variables. Its familiar bell-shaped curve is ubiquitous in statistical reports, from survey analysis and quality control to resource allocation.
Example
The final exam scores in a statistics class were normally distributed with a mean of 63 and a standard deviation of five.
1. Find the probability that a randomly selected student scored more than 65 on the exam.
2. Find the probability that a randomly selected student scored less than 85.
3. Find the 90th percentile (that is, find the score k that has 90% of the scores below k and 10% of the scores above k).
4. Find the 70th percentile (that is, find the score k such that 70% of scores are below k and 30% of the scores are above k).
Solution:
LetX = a score on the final exam. X ~ N(63, 5), where μ = 63 and σ = 5
1. Draw a graph. Then, find P(x > 65). P(x > 65) = 0.3446
The probability that any student selected at random scores more than 65 is 0.3446.
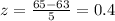
Area to the left is 0.6554.
P(x > 65) = P(z > 0.4) = 1 – 0.6554 = 0.3446
2. Then find P(x < 85), and shade the graph. Using a computer or calculator, find P(x < 85) = 1.normalcdf(0,85,63,5) = 1 (rounds to one)The probability that one student scores less than 85 is approximately one (or 100%).
3. Find the 90th percentile. For each problem or part of a problem, draw a new graph. Draw the x-axis. Shade the area that corresponds to the 90th percentile.
Let k = the 90th percentile. The variable k is located on the x-axis. P(x < k) is the area to the left of k. The 90th percentile k separates the exam scores into those that are the same or lower than k and those that are the same or higher. Ninety percent of the test scores are the same or lower than k, and ten percent are the same or higher. The variable k is often called a critical value.k = 69.4
The 90th percentile is 69.4. This means that 90% of the test scores fall at or below 69.4 and 10% fall at or above. To get this answer on the calculator, follow this step:invNorm in 2nd DISTR. invNorm(area to the left, mean, standard deviation)For this problem, invNorm(0.90,63,5) = 69.4
4. Find the 70th percentile. Draw a new graph and label it appropriately. k = 65.6The 70th percentile is 65.6. This means that 70% of the test scores fall at or below 65.5 and 30% fall at or above.invNorm(0.70,63,5) = 65.6