Question

The base of a right prism is a rhombus with diagonals of 6 and 8. If the altitude of the prism is 12, what is the total surface area of this prism?A. 240 units²B. 288 units²C. 264 units²D. 312 units²

Answer 1

Our prism has 6 faces. 2 equal basis and 4 equal sides. To calculate the area of the base, we just have to use the area formula since we already know the value for the diagonals. To calculate the area of the sides of our prism we have to calculate the side length of the rhombus.

A rhombus has the following properties:

Opposite angles are equal. All sides are equal and, opposite sides are parallel to each other. Diagonals bisect each other perpendicularly.

Since the diagonals bisect each other perpendicularly, half the diagonals and the side of the rhombus form a right triangle.

Using the pythagorean theorem, we can determinate the side length our rhombus.

`\begin{gathered} ((6)/(2))^2+((8)/(2))^2=s^2 \\ 3^2+4^2=s^2 \\ s=√(9+16) \\ s=5 \end{gathered}`

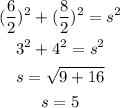
The side length of our rhombus is equal to 5 units. Now that we have all the measures, we can calculate the total surface area. The area of a rhombus is equal to half the product of the diagonals.

`A_b=(6*8)/(2)=(48)/(2)=24`

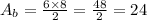
The sides of our prism are rectangles, therefore, the area is given by the product between its distinct sides.

`A_s=12*5=60`

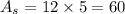
Since we have 4 sides and 2 basis, the total surface area is:

`S=2A_b+4A_s=2(24)+4(60)=48+240=288`

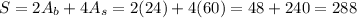
The surface area of our prism is equal to 288 units². The answer is option B.