Question

A polynomial function that describes an enclosure is V(x)=1500x−x2, where x is the length of the fence in feet. What is the maximum area of the enclosure?623,450 ft2375,875 ft2562,500 ft2500,250 ft2

Answer 1

Given polynomial:

`V(x)=1500x-x^2`

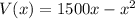
Where x is the length of the fence in feet.

The maximum area of the enclosure can be found by differentiating the polynomial with respect to x and equating to zero.

We have:

`\begin{gathered} V^(\prime)(x)\text{ = 1500 - 2x} \\ 1500\text{ - 2x = 0} \\ 2x\text{ = 1500} \\ \text{Divide both sides by 2} \\ (2x)/(2)\text{ = }(1500)/(2) \\ x\text{ = 750} \end{gathered}`

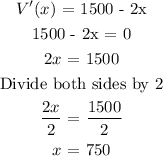
Substituting the value of x back into the enclosure function:

`\begin{gathered} V(x=750)\text{ = 1500 }*750-(750)^2 \\ =\text{ 562500} \end{gathered}`

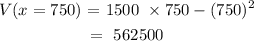
Answer:

562500