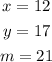Question

Sole the three Pythagorean theorem problems to figure out m

Answer 1

According to the Pythagorean Theorem, if A and B are the legs of a right triangle and C is the hypotenuse, then:

`A^2+B^2=C^2`

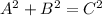
The legs of the first right triangle are 5 and x, and its hypotenuse is 13. Use the Pythagorean Theorem and solve for x:

`\begin{gathered} x^2+5^2=13^2 \\ \Rightarrow x^2+25=169 \\ \Rightarrow x^2=169-25 \\ \Rightarrow x^2=144 \\ \Rightarrow x=\sqrt[]{144} \\ \Rightarrow x=12 \end{gathered}`

The legs of the second right triangle are 8 and x+3. Replace x=12. Then, the legs have measures 8 and 15. Use the Pythagorean Theorem to find the hypotenuse y:

`\begin{gathered} 8^2+15^2=y^2 \\ \Rightarrow64+225=y^2 \\ \Rightarrow289=y^2 \\ \Rightarrow y=\sqrt[]{289} \\ \Rightarrow y=17 \end{gathered}`

The legs of the third right triangle have measures m and 2y-2x+10, and the hypotenuse has length 29. Replace x=12 and y=17. Then, the legs of the third right triangle are m and 20, and the hypotenuse has length 29. Solve for m:

`\begin{gathered} m^2+20^2=29^2 \\ \Rightarrow m^2+400=841 \\ \Rightarrow m^2=841-400 \\ \Rightarrow m^2=441 \\ \Rightarrow m=\sqrt[]{441} \\ \Rightarrow m=21 \end{gathered}`

Therefore, the solutions for x, y and m are:

`\begin{gathered} x=12 \\ y=17 \\ m=21 \end{gathered}`