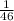Question

Elizabeth brought a box of donuts to share. There are two-dozen (24) donuts in the box, all identical in size, shape, and color. Five are jelly-filled, 4 are lemon-filledand 15 are custard-filled. You randomly select one donut, eat it, and select another donut Find the probability of selecting two lemon-filled donuts in a row.Type an integer get or a simplified fraction

Answer 1

We need to find the probability of selecting two lemon-filled donuts in a row.

That probability is the product of the following:

• the probability of selecting one of the ,4, lemon-filled donuts ,out of 24, donuts (first selection);

• the probability of selecting one of the ,3, lemon-filled donuts that are left ,out of 23, donuts (second selection, after you eat one lemon-filled donut);

Since, in the beginning, there are 4 lemon-filled donuts, and a total of 24 donuts, the probability of selecting a lemon-filled donut the first time is:

`(4)/(24)=(1)/(6)`

Now, given that the first selected one was a lemon-filled donut (eaten by you), there are left only 3 lemon-filled donuts, and a total of 23 donuts.

Thus, the probability of selecting a lemon-filled donut the second time (given you selected a lemon-filled donut the first time) is:

`(3)/(23)`

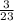
Therefore, the probability of selecting two lemon-filled donuts in a row is given by:

`(1)/(6)\cdot(3)/(23)=(3)/(6)\cdot(1)/(23)=(1)/(2)\cdot(1)/(23)=(1)/(2\cdot23)=(1)/(46)`

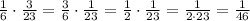
Thus, the answer is:

`(1)/(46)`