Question

Find the area of a trapezoid with bases 24 and 36 with 45 base angles

Answer 1

A trapezoid with congruent base angles have the other two sides (that are not the bases) congruent to each other:

And the area A of a trapezoid with bases a and b, and height h is given by:

`A=(a+b)/(2)\cdot h`

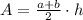
Thus, we need to find the height h of this trapezoid and then use it to calculate its area.

Step 1

We can find h by using the tangent of 45º. We obtain:

`\begin{gathered} (h)/(6)=\tan 45^(\circ) \\ \\ (h)/(6)=1 \\ \\ h=1\cdot6 \\ \\ h=6 \end{gathered}`

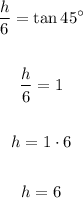
Step 2

Now, we have:

a = 24

b = 36

h = 6

Thus, the area A of the trapezoid is:

`\begin{gathered} A=(24+36)/(2)\cdot6 \\ \\ A=(60)/(2)\cdot6 \\ \\ A=30\cdot6 \\ \\ A=180 \end{gathered}`