Question

sample oft 22 teen were surveyed and asked about how many hours per day they spend grooming themselves assume that self grooming times for teens is normally distributed if the grooming time for these 22 teens was 1.3 hours a day with s= .35are you going to use student t or standard z to help you calculate this confidence interval calculate a 99% confidence interval to estimate the grooming time for all teens

Answer 1

Step 1

State the given data

n= 22 teens

mean = 1.3 hours

standard deviation = 0.35

Step 2

A) State with reason if we are to use t or standard z to calculate the confidence level

Conditions for using t standard include

1) n<30

2) The standard deviation is not given

Since the standard deviation is given we will use the z standard to calculate the confidence level

Step 3

Calculate a 99% confidence interval to estimate the grooming time for all teens

To do this we use the expression

`\bar{x}\pm z_{\propto\text{ }}*\text{ }\frac{s}{\sqrt[]{n}}`

Where

`\begin{gathered} \bar{x}=1.3hours \\ z_{\propto\text{ }}at99percent=2.576 \\ s\text{ = 0.35} \\ n\text{ =22} \end{gathered}`

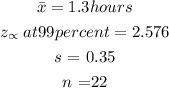
Substituting these value into the equation gives

`\begin{gathered} =1.3\pm2.576_{}*\frac{0.35}{\sqrt[]{22}} \\ =\text{ }1.3\pm2.576(0.07462025) \\ =\text{ 1.3 }\pm0.192221765 \\ So\text{ the interval is 1.3 }\pm0.192221765 \end{gathered}`

So the intervals will be

1.107778235 to 1.492221766