Consider that the mass of water bath is 0.700 kg and the mass of object is 0.200 kg.
The heat required to change the temperature of water is,
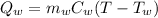
The heat required to change the temprature of object is,
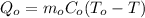
Assume that no heat is lost. Therefore,
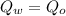
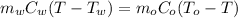
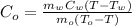
Substitute the known values,

Therefore, the specific heat of lead is 0.833 J/kg.K