Given:
The distance from the tree to the man = 20m.
The angle of elevation is 25 degrees.
The man's eyes are at a height of 2m.
Required:
We need to find the height of the tree.
Step-by-step explanation:
Let h be the height of the tree.
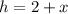
Since 2m is the distance from the ground to the man's eye.
Consider the triangle ABC.
Here Opposite side =BC=x, Adjacent sides = AB=20m,
Use tan formula.
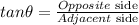
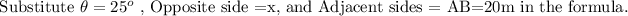
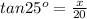

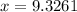
Substitute x =9.3161 in h=2+x .
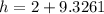
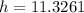
Final answer:
The height of the tree is 11.33 m.