Given the word problem, we can deduce the following information:
Radius = 6 miles
Central angle = 2 radians
To determine the length of the arc, we use the formula:
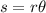
where:
s= arc length
r= radius
θ= central angle in radians
We plug in what we know:
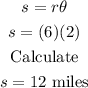
Therefore, the length of the arc is 12 miles.