Answer:
0.1172
Explanation:
The probability that a buyer prefers blue = 50% = 0.5
The number of buyers =10
We want to find the probability that exactly 3 buyers would prefer blue.
To solve this problem, we use the binomial distribution formula given below:
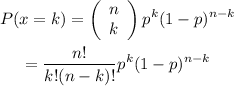
In the given case:
• n=10
,
• k=3
,
• p=0.5
Therefore:

The probability that exactly 3 buyers would prefer blue is 0.1172 (rounded to four decimal places).