We have the next line:

Solve the equation using the slope-intercept form:
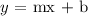
Where m is the slope and b is the y-intercept:
Solving the equation:
-5x - y7 = -8
Add 5x on both sides
-5x + 5x - y7 = -8 + 5x
-7y = -8 +5x
Divide by 7 into both sides:
-7y/7 = (-8 +5x)/7
-y = (-8 +5x)/7
Multiply by -1 to calcel the negative sign:
(-1)(-y) =(-1)* (-8 +5x)/7
y = (8 -5x)/7
y = -5x/7 + 8/7
Now, we need to find the slope of a line perendicular to this line.
"Two lines are perpendicular if and only if their slopes are negative" reciprocals"
So the slope, in this case, is -5x/7
To find the perpendicular line use:
-5x/7 * m = -1
Solve the equation m:
m = (-1)/(-5x/7)
m = 7/5x
So m = 7/5x is the slope of the perpendicular line.
To find the parallel line use:
"Two lines are parallel lines if they do not intersect. The slopes of the"
lines are the same."
So m = -5x/7