Answer:
the triangle is obtuse.
Explanation:
To determine whether the triangle is acute, right, or obtuse, add the squares of the two smaller sides and compare the sum to the square of the largest side.
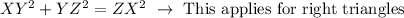
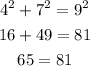
It is not a right triangle, if the sum is greater than the square of the longest side the triangle is acute. But if the sum is less than the square of the longest side the triangle is obtuse.
Therefore, for the given lengths the triangle is obtuse.