The perpendicular line to any other line will have a slope that is the negative reciprocal of the other slope. That means flipping the fraction representing the slope and changing its sign.
To find the slope of a line perpendicular to 6x - 4y = 3 it will be convenient to express this equation in the slope-intercept form to see more clearly the value of its slope. For that we simply isolate the y:

We can clearly see now the slope of the first line:

The slope of the given line 6x -4y = 3 is 3/2.
We know now that the slope of the perpendicular line is the negative reciprocal of 3/2, or well:
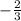
Then, the slope of the line that is perpendicular to the above line is -2/3
Now we can begin building the equation. Recalling the slope-intercept form of the equation of a line:

Where m is the slope of the line, and b is the y-intercept. We know then the value of m:
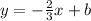
We know that the line passes through the point (6, -1). We can use this information to find the value of b and finish building the equation completely.
We can just find the value of b such that when we replace the x and y-values of the point, the equation is satisfied:

Now knowing the y-intercept we can finally find the equation:
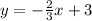
The equation of the perpendicular line that passes through (6, -1) is y = -(2/3)x + 3
.