Question

Find the coefficient of the x^2 term in the expansion of (5x-2)^6 //Series and sequences precalculus

Answer 1

We need to expand the term:

`(5x-2)^6`

This seems like a colossal task, we would need to multiply (5x-2) 6 times. However, we can use a useful tool that is called the 'Pascal's triangle'

I'll paste an image of it above

We will use it in this way:

Each one of the rows, represent the n in the term:

`(x+y)^n`

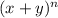
So, if we have the expression (x+y) we will pay attention to the upper row, if we have (x+y)^2 we will need the second row, and so on.

In our case, we need the 6th row.

Now, usually a term of the form

`(x+y)^6=ax^6+bx^5y+cx^4y^2+dx^3y^3+ex^2y^4+fxy^5+gy^6`

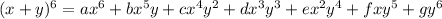
As we say, look at the 6th row of the triangle, the numbers a, b, c,..., and g are given there!

`\begin{gathered} a=1 \\ b=5 \\ c=10 \\ d=10 \\ e=5 \\ f=1 \end{gathered}`

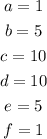
And we need the term that corresponds to x^2, we need the number e=5!

So, after the expansion, the coefficient of the term x^2 will be equal to 5