Question

Describe the vertical asymptote(s) and hole(s) for the graph of y= (x+2) / (x^2+8x+15).a) asymptotes: x = 3 and 5 and hole: x = - 2b) asymptotes: x = 3 and 5 and no holesc) asymptotes: x = - 5, - 3 and hole: x = - 2d) asymptotes: x = - 5, - 3 and no holes

Answer 1

we have the function

`y=(x+2)/(x^2+8x+15)`

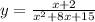
Simplify

`x^2+8x+15=(x+5)(x+3)`

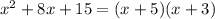
substitute

`y=(x+2)/((x+5)(x+3))`

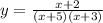
Remember that

The denominator cannot be equal to zero

so

The domain of the given function, are all real numbers, except for x=-5 and x=-3

that means

There are vertical asymptotes at x=-5 and at x=-3

No holes in the graph

therefore

The answer is the option D