ANSWER
20m and 40m
Step-by-step explanation
A rectangular ballroom has two dimensions: length and width,
The perimeter is the sum of all the sides of the rectangle,
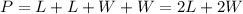
The area is the product of these two dimensions,
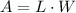
We know that the perimeter is 120m and the area is 800m². Replacing in the equations above, we have two equations with two variables L and W,
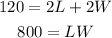
Solve the first equation for W. Subtract 2L from both sides,
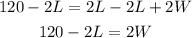
And divide both sides by 2,
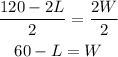
The next step is to replace W by this expression in the second equation,
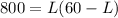
Now we have to solve this equation for L. Apply the distributive property on the right side of the equation,
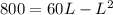
Subtract 800 from both sides,
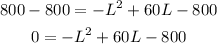
We have a quadratic equation to find the zeros of the polynomial. To solve it, we can use the quadratic formula,
![\begin{gathered} ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/uuterq6bz1kwr2mb9jy58c523r5v4v644y.png)
In this case x = L, a = -1, b = 60 and c = -800,
![L=\frac{-60\pm\sqrt[]{60^2-4\cdot(-1)\cdot(-800)}}{2\cdot(-1)}](https://img.qammunity.org/2023/formulas/physics/college/ec5oiljlhaltj3fn1v7ycfw70s65mcxgjs.png)
![L=\frac{-60\pm\sqrt[]{3600-3200}}{-2}=\frac{-60\pm\sqrt[]{400}}{-2}=(-60\pm20)/(-2)](https://img.qammunity.org/2023/formulas/physics/college/r7duful0gw61pbei01ivl1r81nhy6o5x13.png)
We have two possible results for L,
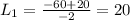
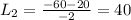
To find the width of the ballroom we have to replace L into the equation we found when we solved the first equation for W,
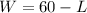
So we have two possible results for W as well,
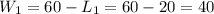
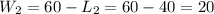
Note that the pairs are 20m and 40m or 40m and 20m. Hence, we can say that the dimensions of the ballroom are 20m and 40m