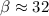Question

Find the angle of elevation of the sun if a 43- foot flagpole cast a shadow 68 feet long. Answer to nearest degree. Draw a picture, write a equation, and solve.

Answer 1

Use the information given in the exercise to draw the following triangle (it is not drawn to scale)

Let be β the angle of elevation of the sun.

Then, knowing that it is a Right Triangle (because it has an angle that measures 90 degrees), you can use the following Inverse Trigonometric Function to find the angle:

`\beta=\tan ^(-1)((opposite)/(adjacent))`

In this case:

`\begin{gathered} opposite=43 \\ adjacent=68 \end{gathered}`

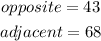
Then, substituting values and evaluating, you get:

`\begin{gathered} \beta=\tan ^(-1)((43)/(68)) \\ \\ \beta\approx32\degree \end{gathered}`

Therefore, the answer is:

- Picture (It is not drawn to scale):

- Equation:

`\beta=\tan ^(-1)((43)/(68))`

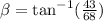
- Solution:

`\beta\approx32\degree`