We have the following:
r = red marbles
g = green marbles
b = blue marbles
y = yellow marbles
the statement gives us the following information
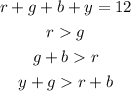
now,
1.
We assume the lowest value for the green ones, that is, 1. For the rest we only have to assume values that conform to the conditions given in the statement
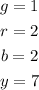
2.
There can only be 2 solutions and the other is the following:
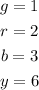
Those are all solutions since if we assume that g equals 2, the conditions cannot be met