Question

Construct sinusoidal functionsThe graph of a sinusoidal function intersects its midline at (0, -3) and then has a maximum point at (2, -1.5).Write the formula of the function, where x is entered in radians.

Answer 1

We have a sinusoidal function.

`y=A\cdot\sin (b\cdot x+c)+d`

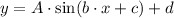
Its midline is intersected at (0,-3) and has a maximum point at (2,-1.5).

As the midline intersects at y=-3, we know that function has an offset of 3 units down.

This offset is the value of the parameter d, so we have:

`y=A\cdot\sin (b\cdot x+c)-3`

The maximum value happens at point (2,-1.5). The maximum value happens when the pure sin function reaches the value 1, so we can write:

`\begin{gathered} y_(\max )=A\cdot1-3=-1.5 \\ A-3=-1.5 \\ A=-1.5+3 \\ A=1.5 \end{gathered}`

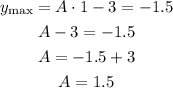
The amplitude is A=1.5, so we can write:

`y=1.5\sin (b\cdot x+c)-3`

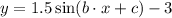
We can find the values of the parameters b and c using the x-values of the the points (0,-3) and (2,-1.5):

`\begin{gathered} (x,y)=(0,-3) \\ y(0)=1.5\sin (b\cdot0+c)-3=-3 \\ 1.5\cdot\sin (c)=-3+3 \\ 1.5\cdot\sin (c)=0 \\ \sin (c)=0 \\ c=0 \end{gathered}`

`\begin{gathered} (x,y)=(2,-1.5) \\ y(2)=1.5\cdot\sin (b\cdot2)-3=-1.5 \\ 1.5\cdot\sin (2b)=-1.5+3 \\ 1.5\cdot\sin (2b)=1.5 \\ \sin (2b)=1 \\ 2b=(\pi)/(2) \\ b=(\pi)/(2)\cdot(1)/(2) \\ b=(\pi)/(4) \end{gathered}`

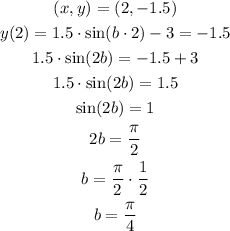
The function becomes:

`y(x)=1.5\sin ((\pi)/(4)x)-3`

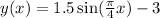
The graph of the function is:

Answer: y(x) = 1.5*sin(pi/4 * x)-3