Given:
A poll is given, showing 80% are in favor of a new building project.
That is, the probability of success is p=0.8
Sample size, n=6
The number of times for a specific outcome within n trials is x=2.
To find the probability that exactly 2 of them favor the new building project:
Using the binomial probability,
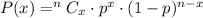
Substituting the given values, we get,
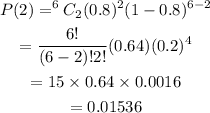
Thus, the probability that exactly 2 of them favor the new building project is 0.01536.