Question

Suppose that $2000 is invested at a rate of 3.4% compounded quarterly. Assuming that no withdrawals are made, find the total amount after 4 years. Do not round any intermediate computations and round your answer to the nearest cent.

Answer 1

Given data:

The amount invested ( principal) is

`P=\text{ \$2,000}`

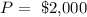
The interest rate given is

`r=3.4\%`

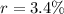
The number of years is

`t=4\text{ years}`

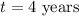
The number of times compounded is quarterly

A quarterly event happens four times a year, at intervals of three months.

`n=4`

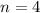
Concept:

The formula to calculate the amount compounded is given below as

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ \text{Where,} \\ A=\text{amount} \\ P=\text{principal} \\ r=\text{rate} \\ n=\text{ number of times compounded} \\ t=\text{ number of years} \end{gathered}`

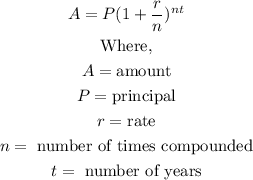
By substituting the values above in the formula, we will have

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ A=2,000(1+(3.4)/(400))^(4*4) \end{gathered}`

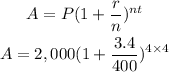
By solving the equation above, we will have

`\begin{gathered} A=2,000(1+(3.4)/(400))^(4*4) \\ A=2,000(1+0.0085)^(16) \\ A=2000(1.0085)^(16) \\ A=2,290.05 \end{gathered}`

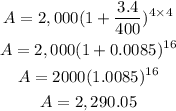
Hence,

The final answer = $2,290.05