Question

Let f(x) = 7x^2 - 7x(a) Use the limit process or derivative to find the slope of the line tangent to the graph of f at x = 4. Slope at x = 4:____(b) Find an equation of the line tangent to the graph of f at x = 4Tangent line: y =

Answer 1

We are given the following function:

`f\mleft(x\mright)=7x^2-7x`

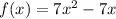
Part A. We are asked to determine the slope of the tangent line at "x = 4".

To determine the slope of the tangent line at a point "x = a" we use the following limit definition:

`m=\lim _(x\rightarrow a)(f(x)-f(a))/(x-a)`

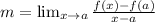
Now, we substitute the value of "x = 4" in the limit definition, we get:

`m=\lim _(x\rightarrow4)(f(x)-f(4))/(x-4)`

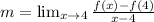
Now, we determine the value of f(4) from the given function;

`f(4)=7(4)^2-7(4)`

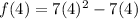
Solving the operations:

`f(4)=84`

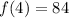
Now, we substitute the values in the limit:

`m=\lim _(x\rightarrow4)(7x^2-7x-84)/(x-4)`

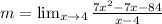
Now, we take 7 as a common factor:

`m=\lim _(x\rightarrow4)(7(x^2-x-12))/(x-4)`

Now, we factor de denominator, we get:

`m=\lim _(x\rightarrow4)(7(x+3)(x-4))/(x-4)`

Now, we cancel out the "x - 4":

`m=\lim _(x\rightarrow4)7(x+3)`

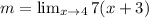
Now, we substitute the values of "x = 4", we get:

`m=\lim _(x\rightarrow4)7(x+3)=7(4+3)=49`

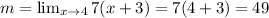
Therefore, the slope is 49.

Part B. We are asked to determine the equation of the tangent line. We have that the general form of a line equation is:

`y=mx+b`

From part A we have that the slope is 49, therefore, we have:

`y=49x+b`

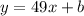
Now, we need to determine a point on the line to determine the value of "b". We already have that the point "x = 4" is part of the line. To determine the corresponding value of "y" we substitute in the given function:

`f(4)=7(4)^2-7(4)`

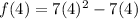
Solving we get:

`f(4)=84`

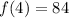
Therefore, the point (x, y) = (4, 84) is on the line. Substituting we get:

`84=49(4)+b`

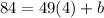
Solving the product:

`84=196+b`

Now, we subtract 196 from both sides:

`\begin{gathered} 84-196=b \\ -112=b \end{gathered}`

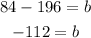
Now, we substitute the value in the line equation:

`y=49x-112`

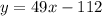
Thus we have determined the equation of the tangent line.