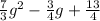You know that the polynomial that represents the inventory of Store A is:
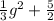
And this polynomial represents the inventory of Store B:
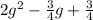
Then, you can set up the following Addition of Polynomials, which represents the combined inventory of Store A and Store B:
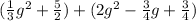
To simplify the expression, you only need to add the like terms (remember that the like terms have the same variables and the same exponents). Then, you get:
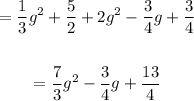
Therefore, the answer is: