Starting from:
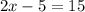
Let's check the first two equations. For this, we want to put "2x" alone in the left side. So let's move "-5" to the other side by adding 5 in both sides:
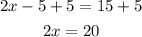
So,
2x = 10 -> incorrect.
2x = 20 -> correct.
To check the thirs one, let's rewrite it and apply the distributive property on the parenthesis:
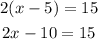
We can see that the right side is the same, but the left side is not, so this is not the same and won't have the same solution.
So,
2(x-5) = 15 -> incorrect.
To check the fourth , we start, again from our equation, we can pass the "1% to the right side:

We can see that it is equivalent to the fourth equation, so it will give the same solution.
So,
2x - 20 = 0 -> correct.
For the fifth, we can see that each term is double the term of the 2x - 5 = 15, so if we divide both sides by 2, we will get the same equation:
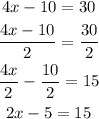
Since the equations are equivalent, they have the same solution.
So,
4x - 10 = 30 -> correct.
The last one has the sides switched, so let's start by switching sides:
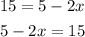
Right side is the same, but the left side is not, because it has inverted sign:
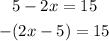
So, this is not equivalent.
So,
15 = 5 - 2x -> incorrect.
So, from the presented equations, the only that have the same solution as 2x - 5 = 15 are:
2x = 20
2x - 20 = 0
4x - 10 = 30