Question

Use slope to determine if lines AB and CD are parallel, perpendicular, or neither 7. A(5.-8), B(-2,-10), C(-6, -13). D(-2.1)m(AB) m(CD) Types of Lines

Answer 1

Tow lines AB and CD are perpendicular to each other if their slope can be related like this:

`m(AB)=-(1)/(m(CD))`

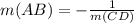
Let's first find the slopes of this lines to see if the formula stated above is

accomplished for this case

The formula of a line has the form:

`y(x)=mx+b`

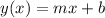
where m, is the slope of the line

The line AB goes through the points (5,-8) and( (-2,-10)

then, y(5)=-8 for the first point, and y(-2)= -10 for the second one.

then:

y(5)= -8=m*(5)+b

and

y(-2)= -10=m*(-2)+b

if we subtract the first expression from the second one we can get:

-8-(-10)=m*5-m*(-2)+b-b, then:

-8+10=2=5*m+2*m=7*m

Then solving for the line AB, m(AB) equals:

`m(AB)=(2)/(7)`

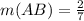
Doing the same for the second line CD that goes through points (-6,-13) and (-2,1), we can find its slope like this:

y(-6)= -13 and y(-2)=1

then:

-13= -6*m+b and 1= -2*m+b

substracting both expressions

-13-1= -6*m - (-2)*m

then:

-14= -4*m

then, for line CD, its slope is:

`m=(-14)/(-4)=(-7)/(-2)=(7)/(2)`

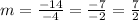
As we can see, m(AC)=2/7 and m(CD)=7/2, then the criteria:

`m(AB)=-(1)/(m(CD))`

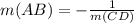
it's not being accomplished, so we can say that these lines are not perpendicular,

Now, lines are parallel when they have the same slope value, which isn't true in this case.

We can say that these lines are neither parallel nor perpendicular