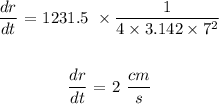Question

A spherical balloon is deflated at a rate of 1231.5 cm^3/sec. At what rate is the radius ofthe balloon changing when the radius is 7 cm?

Answer 1

The radius is changing at a rate of 2 cm/s

Step-by-step explanation:

Here, we want to get the rate at which the radius of the balloon is changing

Mathematically, the formula for the volume of a sphere is:

`\begin{gathered} V\text{ = }(4)/(3)*\pi* r^3^{}^{} \\ \\ (dv)/(dr)\text{ = 4}*\pi* r^2 \end{gathered}`

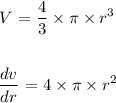
From the question:

`(dv)/(dt)\text{ = 1231.5 }`
`(dr)/(dt)\text{ = ?}`
`(dr)/(dt)\text{ = }(dv)/(dt)*(dr)/(dv)`

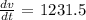
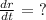
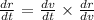
dr/dv is the reciprocal of dv/dr

Thus, we have it that:

`\begin{gathered} (dr)/(dt)\text{ = 1231.5 }*(1)/(4*3.142*7^2) \\ \\ (dr)/(dt)\text{ = 2 }(cm)/(s) \end{gathered}`