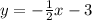
Step-by-step explanation
when you know the slope and a passing point of the line, you can find the equation of the line by replacing in the slope-point equation ,it is given by:
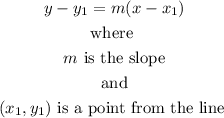
then
Step 1
a)Let
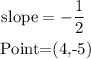
now,replace and solve for y
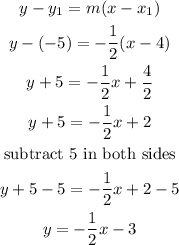
therefore, the answer is
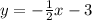
I hope this helps you